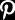DURBAR is a non-slip raised pattern floor plate of integral manufacture (the pattern is rolled in not welded). The “tear drop” studs are distributed to give maximum slip resistance in a variety of applications whilst ensuring a free draining surface.
The nominal gauge of DURBAR is the thickness of the plain plate exclusive of pattern.
Weight per Unit Area
|
Thickness on plain |
Mass |
|
4.5 |
36.9 |
|
6.0 |
48.7 |
|
8.0 |
64.4 |
|
10.0 |
80.1 |
|
12.5 |
99.7 |
Capacity Tables
It is usual to consider floor plates as supported on all four edges although stiffeners or joint covers may only support two edges. If the plates are securely bolted or welded to the supporting system, they may be considered as encastré. This increases the load carrying capacity slightly but reduces the deflection considerably.
The thickness given is exclusive of any raised pattern i.e. on plain.
The breadth is the smaller dimension and the length the greater, irrespective of the position of the main support members.
The maximum uniformly distributed load on the plate (w) is given by Pounder’s formula and the maximum skin stress is limited to the design strength py
For calculating the maximum deflection (dmax) at serviceability, the uniformly distributed imposed load (wimp) on the plate is derived as follows.
w = gdead wdead + gimp wimp
wimp = (w – gdead wdead)/ gimp
For plates simply supported on all four edges
This formula assumes that there is no resistance to uplift at plate corners.
w = a1 py t2 / k B2 [ 1 + a2(1-k) + a3(1-k)2]
dmax = a4 k wimp B4 [1+a5(1-k) + a6(1-k)2] / E t3
Where resistance to uplift at corners is provided, the above formula will be conservative. Higher values may be obtained by assuming encastré status as outlined below.
For plates encastré on all four edges
The plate must be secured to prevent uplift, which would otherwise occur at the plate corners.
w = a7 py t2 / k B2 [ 1 + a8(1-k) + a9(1-k)2]
dmax = a10 k wimp B4 [1+a11(1-k) + a12(1-k)2] / E t3
Where:
L = length of plate (mm) (L > B)
B = breadth of plate (mm)
t = thickness of the plate on plain (mm)
k = L4/(L4+ B4)
py = design strength of plate ( 275 N/mm2 or 355 N/mm2)
E = Young’s modulus (205 x 103 N/mm2)
1/m = Poisson’s ratio (m = 3.0)
gdead = load factor for dead load (1.4)
gimp = load factor for imposed load (1.6)
dmax = maximum deflection (mm) at serviceability due to imposed loads only
w = uniformly distributed load on plate (ultimate) (N/mm2)
wdead = uniformly distributed self weight of plate (N/mm2)
wimp = uniformly distributed imposed load on plate (N/mm2)
a1 to a12 are constants as below
| a1 | = 4/3 |
| a2 | = 14/75 |
| a3 | = 20/57 |
| a4 | = (5m2 -5)/32m2 |
| a5 | = 37/175 |
| a6 | = 79/201 |
| a7 | = 2 |
| a8 | = 11/35 |
| a9 | = 79/141 |
| a10 | = (m2 -1)/32m2 |
| a11 | = 47/210 |
| a12 | = 200/517 |
Information courtesy of Tata Steel.
Note; We do not offer a design and structural calculations. In such cases we recommend that advice is obtained from a suitably qualified structural engineer. It is expressly understood that any technical advice furnished by us with reference to the use of goods is given without charge and we assume no obligation or liability for the advice given or results obtained, all such advice being given and accepted at your own risk. It is the responsibility of the designer or installer to ensure that the products used are fit for purpose. All goods are sold under our standard terms and conditions.